Introduction to Group Theory

The Symmetry Group of the Triangle

There are six motions that can bring an equilateral triangle back into its original position. They are

Do nothing
Rotate 120 degrees counterclockwise
Rotate 240 degrees counterclockwise
Flip about the symmetry axis through the upper vertex
Flip about the symmetry axis through the lower left-hand vertex
Flip about the symmetry axis through the lower right-hand vertex

There are other motions but they are "equivalent" to those listed above. For example rotating the triangle 360 degrees is "equivalent" to doing nothing since the basic orientation of the triangle is unchanged.

We've labelled the vertices A, B and C and have shown the 6 symmetry motions below:

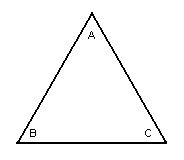
The equilateral triangle before a movement and after any movement
that doesn't change anything (like rotating it 360 degrees).
(Notice the labeling of the corners)

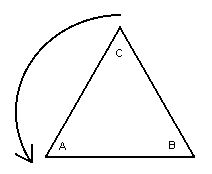
The equilateral Triangle after being rotated 120 degrees counterclockwise
(Note the new locations of vertices A, B and C)

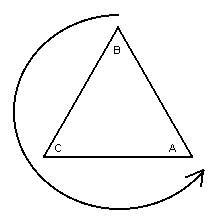
The triangle after being rotated 240 degrees counterclockwise.
(Note the new positions of the vertices A, B and C)

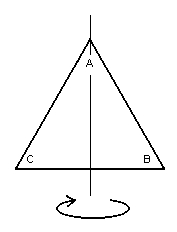
The Triangle after being flipped about the axis through the upper vertex.
(Note the new positions of the vertices A, B and C)

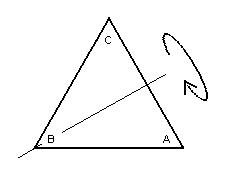
The triangle after being flipped about the axis through the lower left-hand vertex.
(Note the new positions of the vertices A, B and C.)

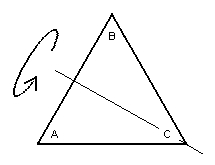
The triangle after being flipped about the axis through the lower right-hand vertex.
(Note the new positions of the vertices A, B and C)

Now we are in a position to combine these symmetry operations of the triangle to form a group. We simply use the operation of followed by and find that

We have closure: performing one motion followed by performing another motion is equivalent (has the same effect) as performing one of the 6 motions.
We have associativity: since followed by is always an associative operation.
We have an identity: The Do nothing motion is the identity element.
We have Inverses: Each element has an inverse:
- The Do nothing is its own inverse.
- The Rotate 120 degrees and the Rotate 240 degrees are inverses of each other.
- The three Flip movements are their own inverses.

It is a good idea to follow the advice of Maria Montessori and involve many senses in your learning. To this end I advise that you make a paper or cardboard triangle and label its vertices A, B and C. Then draw a similar triangle on a piece of paper. Begin with the triangle in the start position (as shown in the first illustration)and perform the various motions, one after another. Note the final orientation of the triangle (by the distribution of its vertices) after the two motions have been performed (one followed by another). What single motion is this equivalent to?

Continuing this way you can fill in a Cayley table for the Symmetry Group of the Equilateral Triangle.

So, let's do it. We'll need some symbols to stand for our movements. So let's let

e stand for the Do nothing movement.
a stand for the Rotate 120 degrees counterclockwise movement.
b stand for the Rotate 240 degrees counterclockwise movement.
X stand for the Flip about axis through the top vertex movement.
Y stand for the Flip about the axis through the lower-left vertex movement.
Z stand for the Flip about the axis through the lower-right vertex movement.

With these definitions for e, a, b, X, Y, and Z we can form the Cayley table for the symmetry group of the equilateral triangle: (In this table the first motion performed is in the left-hand column and the second motion is in the top row.)

• e a b X Y Z

e e a b X Y Z

a a b e Y Z X

b b e a Z X Y

X X Z Y e b a

Y Y X Z a e b

Z Z Y X b a e

Did your table match the one above?? If so give yourself a pat on the back and stick it on the refrigerator.

Subgroups
Back to the Index

Send comments, corrections and criticisms to:

dogschool@dog.com